[프로그래머스] 순위
문제
이해
입력
n (선수의 수)- 타입:
자연수 - 범위:
[1, 100]
- 타입:
results (경기 결과)- 타입:
배열 - 크기:
[1, 4500] - 원소:
- 타입:
배열 - 형태:
[a, b] - 의미: a번 선수가 b번 선수를 항상 이긴다
- 타입:
- 타입:
출력
- 주어진 경기 결과만으로 순위를 정확히 매길 수 있는 선수의 수
조건
- A 선수가 B 선수보다 실력이 좋다면 A 선수는 B 선수를 항상 이긴다.
- 경기 결과에는 모순이 없다.
예시
입력:
n: 5
results: [[4, 3], [4, 2], [3, 2], [1, 2], [2, 5]]
출력:
2
접근
먼저 순위에 대하여 정리해보자. 순위를 매기는 구체적인 방법에 대한 언급은 없으나, 조건 1을 보면 선수의 실력으로 순위를 매기려고 하는 것으로 보인다. 그리고 조건 2에 의해 경기 결과에 모순이 없으므로, 한 번이라도 [A, B]가 나타난다면 A 선수는 B 선수보다 실력이 좋다는 것과, [A, B], [B, A]와 같은 경우는 주어지지 않는다는 것을 알 수 있다.
문제에서 구하고자하는 것은 정확하게 순위를 매길 수 있는 선수의 수이다. 정확하게 순위를 매기려면 나를 제외한 모든 선수와 실력을 비교할 수 있어야 한다. 다시 말해서, 전체 선수의 수가 n명이고 나보다 뛰어난 실력을 가진 선수가 a명, 떨어지는 실력을 가진 선수가 b명이라고 할 때, a + b == n - 1을 만족하는 선수여야 순위를 정확하게 결정할 수 있다. 따라서 위 등식을 만족하는 선수의 수를 구하면 된다.
먼저 생각난 것은 플로이드 워셜 알고리즘이다. 경기 결과를 통해 선수 실력의 우열을 알 수 있고 이를 유향그래프로 표현할 수 있기 때문이다. 예를 들어, [A, B]의 경우 A -> B 와 같이 나타내는 것이다. 이렇게 그래프를 정의하면 A에서 B에 도달 가능하다는 것은 A는 B보다 실력이 뛰어나다는 의미가 된다.
이제 플로이드 워셜 알고리즘을 사용하여 답을 구할 수 있다. 이 알고리즘은 그래프 상의 임의의 두 노드 u와 v에 대하여, u에서 v로 가는 최단 거리를 구하는 알고리즘이다. 단, 이 문제의 경우 최단 거리가 아니라 “도달 여부”만 알아도 충분하다. 왜냐하면 어떤 선수 A의 정확한 순위를 알기 위해서는, A에 도달 가능한 노드의 수와 A에서 도달 가능한 노드의 수를 알면 되기 때문이다.
구현
플로이드 워셜
def solution(n, results):
answer = 0
INF = 987654321
d = [[INF if i != j else 0 for j in range(n)] for i in range(n)]
n_ins = [0] * n
n_outs = n_ins[:]
for s, e in results:
d[s-1][e-1] = 1
for m in range(n):
for s in range(n):
for e in range(n):
d[s][e] = min(d[s][e], d[s][m] + d[m][e])
for i in range(n):
for j in range(n):
if 0 < d[i][j] < INF:
n_outs[i] += 1
n_ins[j] += 1
for i in range(n):
if n_outs[i] + n_ins[i] == n - 1:
answer += 1
return answer
???
다 풀고나서 다른 사람의 코드를 살펴보았는데 나와 다른 풀이가 있었다. (재구현한 코드이다)
def solution(n, results):
answer = 0
parents = {i:set() for i in range(n)}
children = {i:set() for i in range(n)}
for s, e in results:
parents[e-1].add(s-1)
children[s-1].add(e-1)
for i in range(n):
for parent in parents[i]:
children[parent].update(children[i])
for child in children[i]:
parents[child].update(parents[i])
for i in range(n):
if len(children[i]) + len(parents[i]) == n - 1:
answer += 1
return answer
접근 방식이 참신하다고 느꼈다. 특히 업데이트에 대한 발상은 나도 했었는데 제대로 된 풀이법이 떠오르지 않아서 결국 플로이드 워셜을 쓰게 된 것이었다.
이 접근 방법의 경우 모든 노드가 자신의 조상과 후손에 대한 정보를 계속 끌고 다닌다. 그리고 업데이트를 통해 서로의 정보를 알고 있는 군집을 확대시키게 된다. 군집끼리 만나면 정보가 퍼지며 하나의 군집으로 뭉쳐진다. 예를 들어 다음과 같은 상황을 보자.
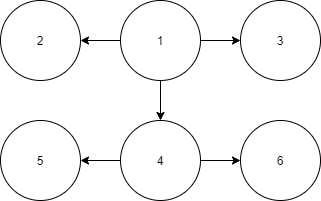
1은 5, 6에 도달할 수 있다. 그러나 주어진 정보로 초기화된 1은 그 사실을 알 수 없다. 이 상황에서 4를 업데이트하게 되면 4의 모든 조상에게 4의 모든 후손의 존재를 알리게 된다. 이 과정에서 1은 5와 6의 존재를 알게 된다.
더 나아가서 위의 상황에서 1의 부모를 가정해보자. 1을 업데이트하게 되면 후손인 2, 3, 4, 5, 6의 정보가 1의 부모에게 전파된다. 그런데 만약 4보다 1을 먼저 업데이트하면 어떻게 될까? 이 경우 1이 5, 6을 모르는 상황이므로 당연히 1의 부모도 5, 6이 있는지 모른다. 그러나 4는 1의 부모가 있다는 사실을 알게 된다. 후에 4를 업데이트하게 되면 4는 자신의 조상에게 자신의 후손 정보를 전파하게 되는데 그 과정에서 1의 부모에게도 전파가 된다. 이렇게 위아래 양방향으로 전파하기 때문에 업데이트 순서와 무관하게 정보를 업데이트할 수 있다.
이 방식은 노드마다 정보를 저장해야 하므로 많은 메모리를 소비하지만 $n^2$ 이하의 시간 복잡도를 가지므로 $n^3$인 플로이드 워셜보다 훨씬 빠르게 동작한다.

댓글남기기