[프로그래머스] 압축

문제

출처

이해

입력

• 압축할 문자열 msg
  • 배열 크기: [1, 1000]
  • 원소 범위: [A, Z]
  • 원소의 의미: 알파벳

출력

• LZW 알고리즘으로 압축된 문자열

규칙

1. 주어진 문자열을 LZW 알고리즘으로 압축한다.
   • LZW 알고리즘
     1. 압축 대상 문자열을 구성하는 길이가 1인 모든 문자를 사전에 등록한다.
        • {A: 1, B: 2, ... Z: 26}
     2. 사전에서 현재 입력과 (앞에서부터) 일치하는 가장 긴 문자열 w를 찾는다.
     3. w에 해당하는 사전의 색인 번호를 출력하고 주어진 문자열에서 제거한다.
     4. 주어진 문자열이 남아있다면 w + <주어진 문자열의 첫글자>를 사전의 마지막에 등록하고 2번으로 돌아간다.

예시

입력
msg: "KAKAO"

출력
[11, 1, 27, 15]

접근

이 문제는 특별한 알고리즘이 필요하지 않고 주어진 pseudo-code를 구현하면 되는 문제이다. 다만 선형탐색으로 문자열을 비교하는 대신 hash table 기반 자료형인 dictionary를 사용하면 더 빠르게 동작하는 코드를 쉽게 작성할 수 있다.

구현

선형 탐색

def solution(msg):
    answer = []
    # 참고로 ord는 문자를 ascii로, chr는 ascii를 문자로 바꾸는 내장 함수이다.
    n_li, li = 27, [(chr(i + ord('A')), i+1) for i in range(26)]
    now = ''
    
    def get(s):
        for (k, v) in li:
            if s == k:
                return v
        return None
    
    for c in msg:
        nxt = now + c
        if get(nxt):
            now = nxt
        else:
            answer.append(get(now))
            li.append((nxt, n_li))
            n_li += 1
            now = c
    answer.append(get(now))
    return answer

해시 테이블

def solution(msg):
    answer = []
    n_dt, dt = 27, {chr(i + ord('A')):i+1 for i in range(26)}
    now = ''
    
    for c in msg:
        nxt = now + c
        if nxt in dt:
            now = nxt
        else:
            answer.append(dt.get(now))
            dt[nxt] = n_dt
            n_dt += 1
            now = c
    answer.append(dt.get(now))
    return answer

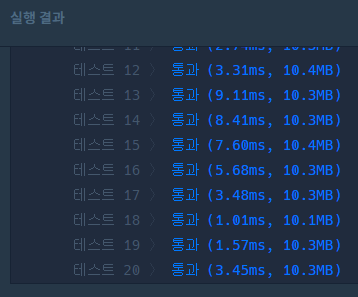
성능 비교

선형 탐색

해시 테이블

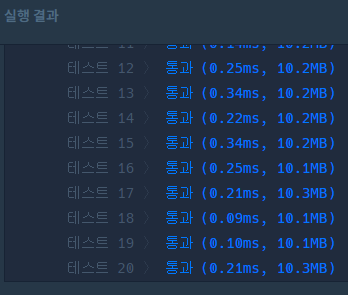
해시 테이블을 사용한 코드가 더 빠르게 동작함을 알 수 있다.